2021-02-19 15:16
目前,使用 LP Token 进行抵押借贷的需求越来越大,但是目前市面上并没有一种完善的用于安全获取 LP Token 价格的方法。慢雾安全团队在分析 LP Token 价格的获取方式的过程中关注到了 Alpha Finance 团队的关于安全获取 LP 价格的方法。在仔细阅读后,将相关的思考分享给大家。
目前,常见的 LP Token 价格的获取方式如下:
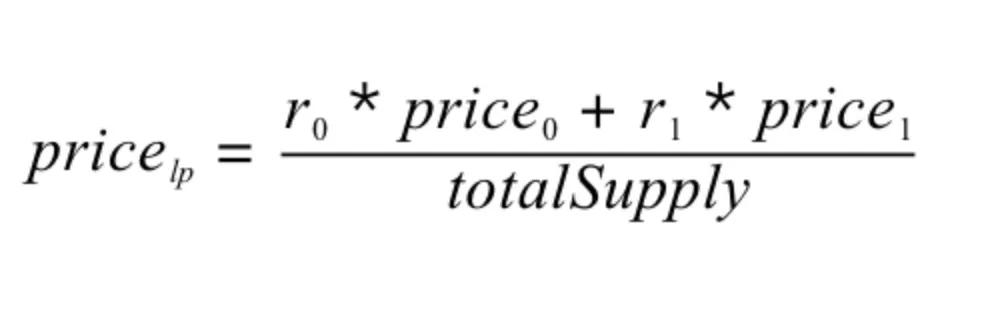
其中,r0,r1 分别代表 Uniswap 交易对中两种代币的存量,price0,price1 分别代表 r0 和 r1 对应代币的价格。上面的公式简单来说就是算出交易对中两种代币的总价值之和,然后除以 LP Token 的总数量,得到了单份 LP 的价值。
这个公式咋一看没什么问题,一般来说,price0 和 price1 都会取 Uniswap 本身提供的延时价格。但是这里存在一个被闪电贷攻击的风险。虽然 price0 和 price1 是不能操控的,但是 r0 和 r1 却是可以操控的。通过操控 r0 和 r1 的值,即可对整个公式进行操控。
那么有没有办法能获取一种安全的 LP Token 价格,使代币的存量无法被操控呢?Alpha Finance 团队提供了一个思路:

根据 Alpha Finance 的分析,整个过程分为 3 步:
第 1 步是通过 Uniswap 的 getReserves 接口获得交易对中对应代币的数量,算出 K
第 2 步是获取交易对中每个代币对应的价格,然后算出代币的价格的比例 P
第 3 步是通过 K 和 P 之间的关系反推真实的代币存量。
完成以上 3 步后,最终 LP Token 的价格获取公式会变成下面这个样子:

这一波操作下来,好像有点整懵了,但是问题不大,我们来逐个分析。
首先,我们知道,Uniswap 采用的是恒定乘积算法。简单来说就是 x * y = K ,也就是说,交易前后的 K 值是不会变的。在不讨论手续费的情况下,K 值理论上是不会改变的。我们先记住这个前提。然后,获取交易对中每个代币各自的价格,比方说对 USDT 价格。这里以 ETH-BTC 交易对为例,假设 ETH 的价格为 650 USDT,BTC 的价格为 22,000 USDT,那么 ETH/BTC 的价格比值 P 为 0.03。在得到价格的比值 P 之后,直接用第 1 步得到的 K 计算 K/P 和 K*P 就得到了对应交易对的一个正常的数量。下面要对第 3 步,即获取正常的数量这一步进行相应的说明。
现在开始对上面的第 3 步进行说明,扶稳坐好 :D
像前面说的,恒定乘积的公式为:
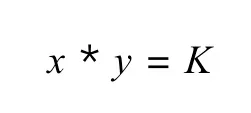
那么其实可以根据 K 来分别算出 x,y。然后根据上一节的第 2 步,我们得到了 x 和 y 的价格的比值 P。由于 Uniswap 本身是根据池中代币的比例来确定对应的价格,所以比值 P 本身就是 x/y 的价格的比值。然后,由于 K = x * y,而 P 是由正确的价格算出的比值,那么,我们其实就可以以这个真实的 K 和 x/y 来反推真实的 x 和 y 。
推算如下:
首先,我们根据 P 和 r0,r1 的比例得出以下公式:
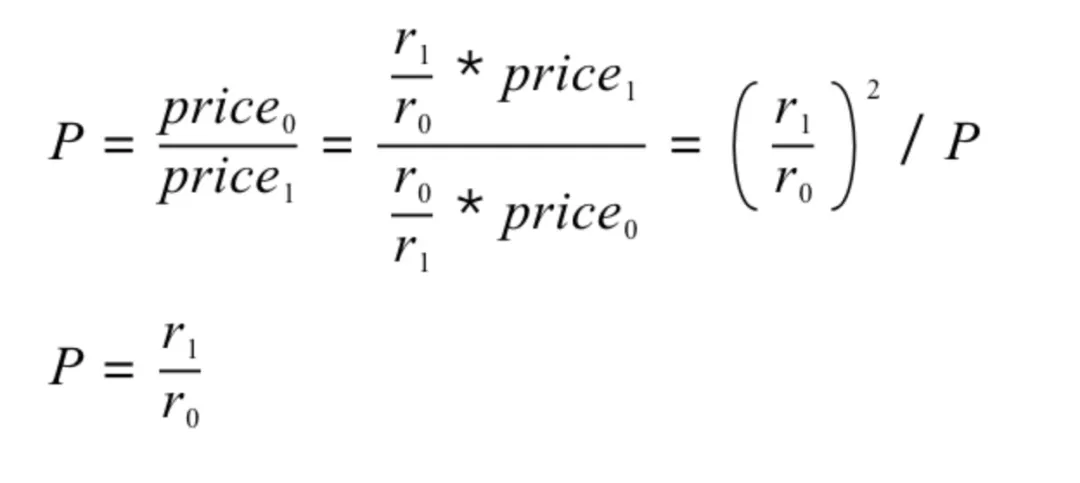
接着,根据 P 就可以倒推真实的 r0,r1,如下:
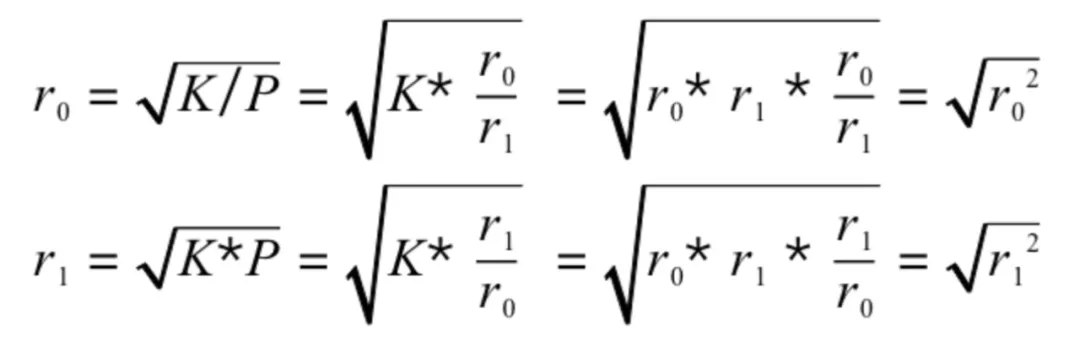
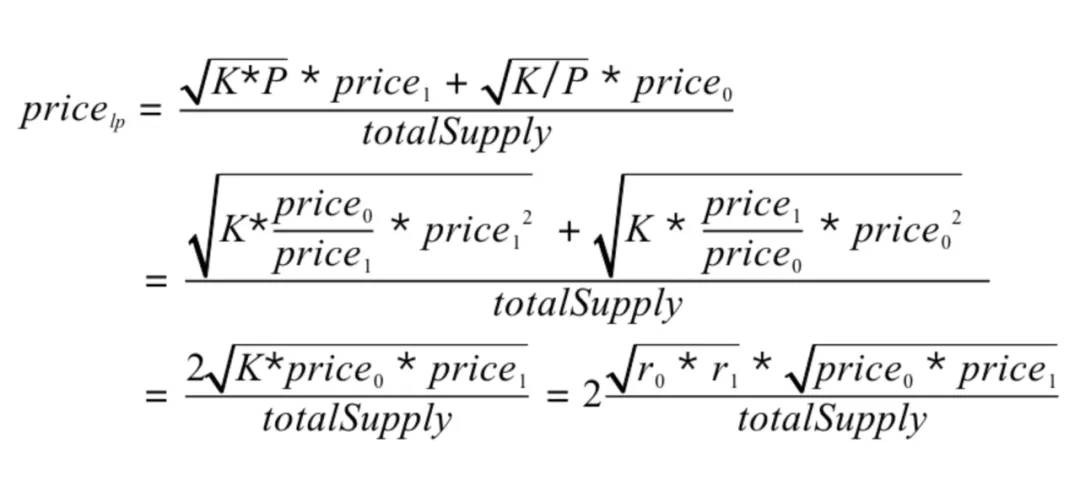
那么,拿到了正确比例的 x 和 y 之后,LP 的价格会是下面这个公式:
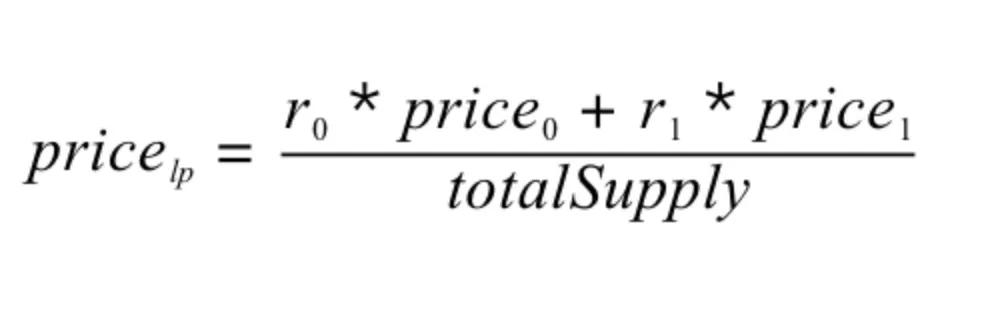
再转换成如下:
在完成公式分析后,我们不难知道,只要有正确的价格的比例 P,就能根据这个比例倒推真实的 r0 和 r1,最后得到公式:
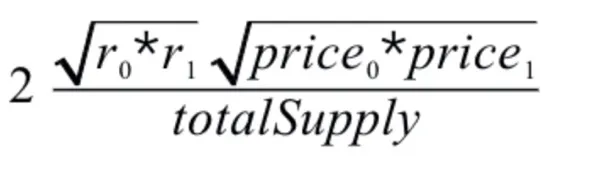
那么,这个公式能不能被攻击呢?从公式上可以知道,公式的 price0,price1 都是可信源获取的正确的价格,这个值是无法被操控的,然后是 totalSupply,这个值虽然可以操控,但是在控制 LP 价格进行攻击的过程中改变 totalSupply 只能是改变你的抵押数量,这个暂时没有用。那么剩下可以操控的只有 r0 和 r1 的值了。如何改变 r0,r1 的值呢?下面提供两种思路进行分析:
思路一:直接进行代币兑换
我们知道,在代币池中,无论是采用什么算法进行计算,代币池在进行代币兑换的过程中,必然会发生代币数量的改变,那么这种改变最终能不能操控公式呢?其实是不可以的。我们知道,在恒定乘积的模型中,x * y = K 总是成立的,那么也就是说无论交易过程中怎么发生代币的兑换,K 的值总是不变的(这里不考虑手续费的情况),而公式中采用的是 r0 和 r1 进行相乘,所以使用代币兑换来操控公式实际上是不可行的。
思路二:将代币直接打入到代币池中
这种思路比较粗暴,可以直接忽视 K 值来操控 r0 和 r1 相乘的值,但是经过我的运算,这种方法看似可行,其实是不行的。虽然达到了操控的目的,但是因为公式本身在获取最终价格的时候采用的是根号的模式,所以最后获得的收益是根号后的收益,比方说付出 10,000 的成本,最后只能获得最多 100 的收益,这样是明显不划算的。所以这种思路也是不可行的。
本算法的适用范围仅限于适用 AMM 模型的代币池的 LP 价格的获取,因为整个推导过程都基于恒定乘积公式中 K 的基本特性来进行。获取的 LP 本身所属的交易对算法不使用 AMM 模型是不可行的,因为这种情况下,前面所有的假设都已经不成立了,那么对应的公式的推算自然也是不成立的。
LP 抵押已经成为了一种迫切的需求,在目前没有更好的方式(如 ChainLink 提供的 LP 喂价,Uniswap 提供延时 LP 接口等),Alpha Finance 的方式可以说是一种较为安全的实现方法,使针对数量进行控制的攻击变成不可行或成本非常高。当然,随着越来越多场景的出现,这种算法也不一定是万能的,项目方需要结合自身的场景,合理运用该算法,达到良好的效果。此外,特别需要注意的是,虽然公式的终极形式用的是开根号的 r0,r1 和 price0,price1 相乘,但是真正实现的时候,需要根据 K 来推导具体的 r0 和 r1 的值,不然会存在一定的误差。
来源:慢雾科技










Dear users, due to policy restrictions, mainland China IP addresses will be forbidden to access this website, registration and use are prohibited. If you are a mainland China user, please exit safely, if you continue to use the risks caused The responsibility and responsibility will be solely borne by you. At the same time, the platform has the right to refuse to provide services. Thank you for your understanding, please accept and agree!